Back-to-Basics: Multiskalen-Materialmodelle für kurzfaserverstärkte Kunststoffe

Was ist Multiskalen-Modellierung?

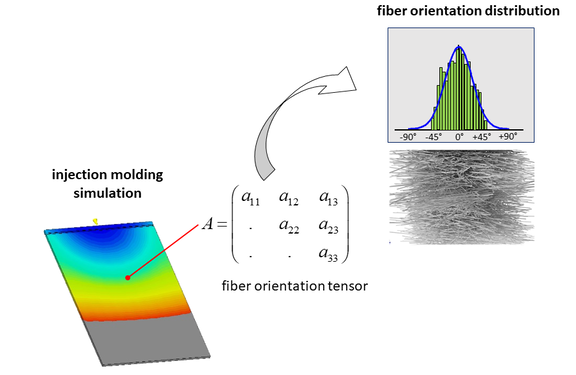
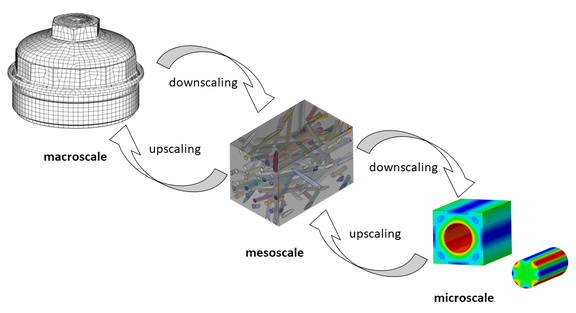
Multiskalen-Modellierungsansätze finden in der Struktursimulation zunehmend Anwendung. Mittels solcher Ansätze kann das Werkstoffverhalten von inhomogenen Werkstoffen beschrieben werden. Insbesondere werden solche Modelle für spritzgegossene kurzfaserverstärkte Kunststoffe angewendet. Die Idee hierbei ist, die komplexe Werkstoffstruktur im Bauteil durch Wechsel des Längenskalenbereichs (Lokalisation oder downscaling) soweit aufzulösen, dass die Zusammenhänge im höher aufgelösten Längenskalenbereich (Mikro- bzw. Meso-Ebene) einer mathematischen Beschreibung besser zugänglich sind (Bild 1).

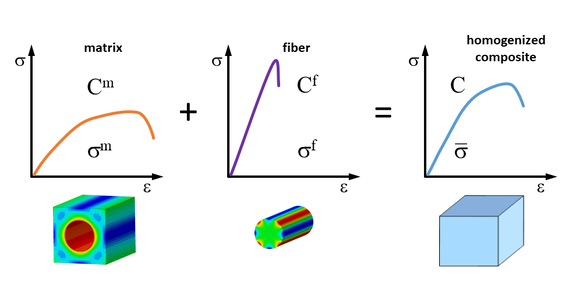
So ist es möglich das Verhalten eines Verbundwerkstoffs nur auf der Grundlage der Materialeigenschaften seiner Bestandteile, also Matrixpolymer und Verstärkungsfaser zu berechnen. Die Bestandteile mit ihren spezifischen Eigenschaften und ihrer räumlichen Konfiguration bestimmen dann das Materialverhalten des Verbundwerkstoffs auch auf der makroskopischen Bauteilebene (Bild 2).

Aus Effizienzgründen ist es nun nicht angemessen, ein komplettes Bauteil durch vollständige Modellierung seiner Mikrostruktur abzubilden. Aus diesem Grunde erfolgt eine sogenannte Homogenisierung (upscaling). Hierdurch werden ausgehend von den Eigenschaften des inhomogenen Werkstoffs auf der Mikro- bzw. Meso-Ebene, äquivalente homogenisierte Eigenschaften (z.B. Steifigkeiten) ermittelt. Im Weiteren wird der Werkstoff dann als homogenes Kontinuum aufgefasst. Im Falle einer Kurzfaserverstärkung weist der homogenisierte Werkstoff dann analoges anisotropes Verhalten auf, wie der real inhomogene Verbundwerkstoff. Die homogenisierten Materialkennwerte können dann verwendet werden, um numerisch effizient eine FEM-Analyse des Bauteils durchzuführen. Die Werkstoffmodellierung auf der Mikro- bzw. Meso-Ebene inklusive der Homogenisierung kann auf unterschiedliche Art und Weise erfolgen. Hierin unterscheiden sich im Wesentlichen die verschiedenen Multiskalen-Modellierungsansätze. Im Folgenden werden einige der häufig angewendeten Ansätze vorgestellt.

Verschiedene Multiskalen-Ansätze

Die Basis der Ansätze ist die Festlegung eines sogenannten repräsentativen Volumenelements (RVE). Das RVE stellt dabei einen Ausschnitt aus der makroskopischen Bausteilstruktur dar. Einerseits muss das RVE die typische Mikrostruktur des Werkstoffes so weit umfassen, dass bei einer weiteren Vergrößerung des Volumenausschnittes sich dessen äußeren mechanischen Eigenschaften nicht mehr verändern. Es muss im statistischen Sinne repräsentativ sein, also eine sinnvolle Mittelung im betrachteten Bereich erlauben. Andererseits muss das RVE kleiner als die charakteristischen Abmessungen des Bauteils sein. Für ein Bauteil müssen in der Regel mehrere RVEs definiert werden, da sich infolge der Faserorientierung auch die lokale Mikrostruktur im Bauteil unterscheidet.

Grundlegend lassen sich die Multiskalen-Modellierungsansätze in numerische und in analytische Verfahren unterscheiden. Beide Vorgehensweisen werden im Folgenden exemplarisch dargestellt.

Numerische Multiskalen-Ansätze

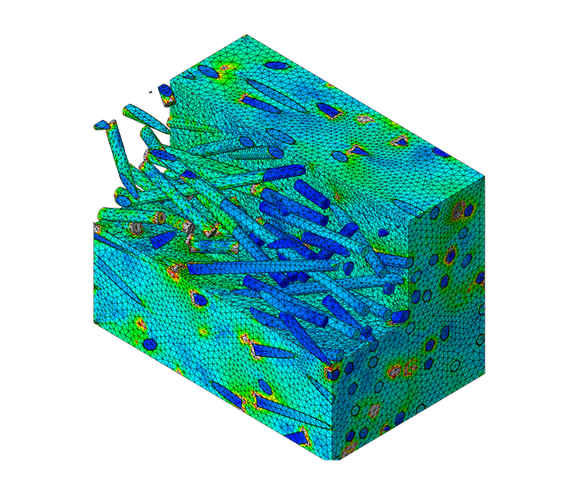
Numerische Multiskalenmodelle bilden auf der Meso-Ebene die reale Mikrostruktur in einem definierten Ausschnitt des Bauteils ab, dem RVE (Bild 3). Üblicherweise werden hierfür FE-Modelle verwendet. Die Herausforderung dabei ist die Mikrostruktur ausreichend genau abzubilden und gleichzeitig die Modellgröße in einem akzeptablen Rahmen zu halten. Damit das Modell repräsentativ für den betrachteten Bauteilausschnitt ist muss eine ausreichende Anzahl von Fasern modelliert werden, z.B. 100 Fasern. Diese werden dann randomisiert entsprechend der angenommenen räumlichen Faserorientierungsverteilung (Winkelklassen) im Volumen verteilt. Es werden periodische Randbedingungen auf die Begrenzungsflächen des RVE aufgeprägt. Die Verschiebungsrandbedingungen der sich jeweils gegenüberliegenden Flächen des RVE sind gekoppelt. Dies wird der Annahme gerecht, dass sich die Ausschnitte der Mikrostruktur im Bauteil aneinanderreihen.

Auf das RVE können nun makroskopische Verschiebungen aufgeprägt werden, die z.B. aus der entsprechenden Position im Bauteil über eine FE-Analyse erhalten werden. Wiederum mittels einer FE-Analyse des RVE wird die Dehnungs- und Spannungsverteilung im RVE ermittelt. In einem weiteren Schritt erfolgt dann eine Homogenisierung über eine Volumenmittelung der Dehnungs- und Spannungsverteilung im RVE:

 (1)

mit: ε Dehnungstensor, σ Spannungstensor, V Volumen, ( ¯ ) volumengemittelte Werte

Hieraus ergibt sich dann der gemittelte Steifigkeitstensor:

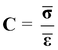  (2)

mit: C volumengemittelte Verbundsteifigkeit

Dieser kann dann wieder an die FE-Simulation des Bauteils übergeben werden zur Berechnung des nächsten Lastschritts.

Aufgrund der ineinander geschachtelten FE-Analysen von Bauteil und RVE wird auch die Bezeichnung FE² für diese Vorgehensweise verwendet. Dies lässt auch schon auf den hohen numerischen Aufwand schließen. Aus diesem Grunde wurden verschiedene Varianten der Vorgehensweise entwickelt. Bei linear-elastischem Werkstoffverhalten ändert sich der Steifigkeitstensor über den Lastschritten nicht. Hier kann mit bereits vor-analysierten RVEs gearbeitet werden, deren Steifigkeiten dann in einer Datenbank abgelegt sind und der jeweiligen lokalen Mikrostruktur im Bauteil zugewiesen werden. Anstatt einer FEM-Analyse des RVE kann auch mit einem voxel-ähnlichem strukturiertem Netz gearbeitet werden, dass mittels eines sogenannten FFT-Solver gerechnet wird. Hierdurch kann die Rechenzeit für das RVE erheblich reduziert werden. Auch gibt es Ansätze, die numerische RVEs nutzen, um damit ein neuronales Netz (künstliche Intelligenz) zu trainieren. Das neuronale Netz liefert dann ein analytisches Modell für das mechanische Verhalten des RVE, das numerisch effizient an die Simulation des Bauteils übergeben werden kann.

Numerische RVEs weisen grundsätzlich keine Einschränkungen hinsichtlich der Materialbeschreibung auf. Neben linear-elastischem Materialverhalten, kann auch plastisches und viskoelastisches Verhalten dargestellt werden. Weiterhin kann im Rahmen der Versagensbewertung eine hohe Auflösung hinsichtlich der Schadensursache und -lokalisation erfolgen. So kann beispielsweise differenziert werden zwischen Faserbruch, Matrixbruch und Faser-/Matrix Ablösung. Der Preis hierfür ist allerdings der hohe Modellierungsaufwand und sehr lange Rechenzeiten, so dass eine Analyse kompletter Bauteile mit diesem Ansatz zumindest zurzeit nicht praxisgeeignet ist.

Analytische Multiskalen-Ansätze

Historisch betrachtet basieren die heute bekannten analytischen Multiskalen-Ansätze auf mikromechanischen Modellen, die seit vielen Jahrzehnten bekannt sind. Alle Verfahren haben auch hier zum Ziel einen physikalisch inhomogenen Werkstoff zu homogenisieren und gemittelte mechanische Eigenschaften zu liefern, die äquivalentes Verhalten aufweisen wie der inhomogene Werkstoff. Im Zusammenhang mit analytischen Multiskalen-Ansätzen wird hierbei auch von Mean-Field-Homogenisierung (MFH) gesprochen. Damit wird zum Ausdruck gebracht, dass mechanische Feldgrößen wie Dehnung und Spannung im RVE gemittelt werden, um die effektive Steifigkeit des homogenisierten Verbundwerkstoffs zu berechnen.

Mischungsregeln

Die einfachsten Modelle sind Mischungsregeln, die aus dem Faservolumenanteil und den Steifigkeiten von Faser und Matrix die Steifigkeit bzw. Nachgiebigkeit des Verbundwerkstoffes berechnen. Zu nennen sind hier die Ansätze von Voigt und Reuss:

  (3)

  (4)

mit: C Steifigkeitstensor, Nachgiebigkeitstensor, ν_f Volumenanteil Faser, ν_m = (1-ν_f) Volumenanteil Matrix

Da in der Regel eher der Fasergewichtsanteil bekannt ist, kann der Faservolumenanteil wie folgt berechnet werden:

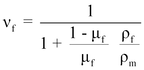  (5)

mit: μ Gewichtsanteil, ρ Dichte

Voigt geht in seinem Ansatz davon aus, dass Faser und Matrix im RVE identische Dehnung erfahren, Reuss hingegen geht von einer identischen Spannung aus. Voigt berechnet demzufolge die Steifigkeit des Verbundes, Reuss hingegen die Nachgiebigkeit. Der Ansatz nach Reuss wird auch als inverse Mischungsregel bezeichnet. Da in beide Modelle keine Informationen über die Fasergeometrie eingehen, sind sie für geometrisch gerichtete (nicht kugelförmige) Einschlüsse nur grobe Näherungen. Der Voigt-Ansatz ist dabei eine obere Grenze und der Reuss-Ansatz eine untere Grenze für die Verbundsteifigkeit.

Modelle auf Basis der Eshelby-Theorie

Es existieren eine Reihe von leistungsfähigeren Modellen, als die oben beschriebenen Mischungsregeln, die auch unterschiedliche Fasergeometrien berücksichtigen können und deutlich bessere Vorhersagen der Verbundeigenschaften auch anisotroper Werkstoffe erlauben. Zu den bekanntesten Modellen gehören diejenigen auf der Basis der Arbeiten von Eshelby (1957). Der Ausgangspunkt der Eshelby-Theorie ist ein RVE bestehend aus einem ellipsoiden Einschluss, im Falle von kurzfaserverstärkten Kunststoffen, einer einzelnen Faser, umgeben von einer unendlich ausgedehnten Matrix.

Ein grundlegendes Konzept der Theorie ist die Einführung sogenannter Dehnungs- und Spannungskonzentrationstensoren A und B. Dies sind die Verhältnisse zwischen der gemittelten Dehnung (Spannung) in der Faser und der korrespondierenden gemittelten Werte im Verbundwerkstoff:

  (6)

  (7)

mit: A Dehnungskonzentrationstensor, B Spannungskonzentrationstensor

Die Konzentrationstensoren A und B haben die Aufgabe, die makroskopischen äußeren   Dehnungen und Spannungen  am Rand des RVEs auf die lokalen gemittelten Dehnungen  und Spannungen  in der Faser zu transformieren. Die gemittelte Verbundsteifigkeit lässt sich dann über folgende Beziehung berechnen:

  (8)

Die volumengemittelte Steifigkeit C des Verbundwerkstoffes berechnet sich auf diese Weise aus den bekannten Steifigkeiten für Faser- und Matrixwerkstoff C^f und C^m, dem Faservolumenanteil ν_f  und dem Konzentrationstensor A. Es verbleibt demnach letztlich nur die Frage, wie der Konzentrationstensor A zu ermitteln ist. Hierzu liefert die Literatur verschiedene Vorgehensweisen.

Eshelby gibt den Dehnungskonzentrationstensor A wie folgt an:

  (9)

mit: I Einheitstensor, E Eshelby-Tensor

Der Eshelby-Tensor E berechnet sich aus den bekannten Werten von Steifigkeitstensor der Matrix C^m und Längen/Durchmesser-Verhältnis der Faser. Somit sind alle Größen zur Berechnung der Verbundsteifigkeit bekannt. Allerdings ist die Berechnung der Verbundsteifigkeit mittels des Dehnungskonzentrationstensors A^Eshelby nur bis Faservolumenanteile von ca. 1 % genau. Man spricht deshalb in diesem Zusammenhang auch von dem verdünnten (dilute) Eshelby-Modell. Dies ist folglich für praxisrelevante kurzfaserverstärkte Kunststoffe nicht direkt anwendbar.

Aus diesem Grund wurde von Mori und Tanaka eine alternative Definition des Dehnungskonzentrationstensors A für nicht-verdünnte (non-dilute) Werkstoffe vorgeschlagen, die für die Modellierung kurzfaserverstärkter Kunststoffe häufig angewendet wird. Die Grundidee von Mori und Tanaka ist, dass eine Faser um sich herum nur Eigenschaften der Matrix sieht und nicht die des homogenisierten Verbundwerkstoffs (siehe Gl. (6)):

  (10)

Die Fasern liegen also so weit auseinander, dass sie keine Rückkopplung untereinander haben. Unter Verwendung der fundamentalen Lösung von Eshelby für die mechanischen Beziehungen einer einzelnen Faser eingebettet in einer (unendlich ausgedehnten) Matrix kann unter dieser Annahme der Dehnungskonzentrationstensors AMT von Mori und Tanaka berechnet werden zu:

  (11)

Mit dem Dehnungskonzentrationstensors A^MT und Gl. folgt damit schließlich die gesuchte Steifigkeit des Verbundwerkstoffes. Die Gleichung gilt zunächst für beliebiges Werkstoffverhalten in Faser und Matrix, da für die Steifigkeitstensoren C^fund C^m bislang keine Einschränkungen getroffen wurden. Unter der einschränkenden Annahme linear-elastischen Werkstoffverhaltens geben Tandon und Weng eine analytische Lösung an, mit der die Verbundsteifigkeit in Form der Ingenieurkonstanten direkt berechnet werden können. Wird jedoch z. B. die Matrix elasto-plastisch beschrieben, so folgt im Allgemeinen immer ein anisotroper Steifigkeitstensor. In diesem Fall kann keine analytische Lösung angegeben werden, die Verbundsteifigkeit muss iterativ numerisch ermittelt werden.

Eine für die Praxis bedeutsame Einschränkung der Mori-Tanaka-Theorie, und alle darauf aufbauenden Beziehungen, ist in der Annahme begründet, dass eine Faser nicht mit einer benachbarten Faser gekoppelt ist. Damit gilt streng genommen der Mori-Tanaka-Ansatz nur für geringe Faservolumengehalte. Die Praxis zeigt jedoch, dass der Mori-Tanaka-Ansatz auch für Faser-Volumenanteile von 30 % und mehr erfolgreich angewendet werden kann.

Orientierungsmittelung

Dadurch, dass der Mori-Tanaka-Ansatz auf der Eshelby-Lösung basiert, gilt die Beziehung zunächst nur für Mikrostrukturen, bei denen die Fasern im betrachteten repräsentativen Volumen alle in die gleiche Richtung, also unidirektional, ausgerichtet sind (transversal isotrop). Dieses ist für reale Mikrostrukturen in spritzgegossenen Formteilen nicht der Fall. Vielmehr liegt eine räumliche Faserorientierungsverteilung vor. Neben der oben mittels der verschiedenen Verfahren dargestellten Volumenmittelung der Verbundsteifigkeit muss in einem zweiten Schritt noch eine Mittelung der Verbundsteifigkeiten über die verschiedenen Faserorientierungs-Winkelklassen durchgeführt werden. Man spricht in diesem Zusammenhang von einer 2-Stufen-Homogenisierung. Das Ergebnis aus beiden Stufen ist das eine homogenierte effektive Gesamtsteifigkeit des Verbundes für die vorliegende Faserorientierungsverteilung (Bild 4).

Die Gesamtsteifigkeit des Verbundes berechnet sich dann zu:

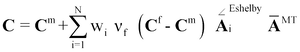 (12)

mit: w_i Gewichtung pro Winkelklasse,  Dehnungskonzentrationstensor in lokales Elementkoordinatensystem transformiert, gemittelter Dehnungskonzentrationstensor

Die Gewichtungsfaktoren w_i werden aus der Rekonstruktion der Orientierungsverteilungsfunktion erhalten, die nachfolgend noch beschrieben die. Die in Gl. angegebene Art der Homogenisierung wird sogenannte Full-Mori-Tanaka Homogenisierung bezeichnet im Gegensatz zur sogenannten Pseudo-Grain-Homogenisierung. Bei der Pseudo-Grain-Homogenisierung werden nicht nur die Fasern in verschiedene Faserwinkelklassen unterteilt, sondern auch die umgebende Matrix (grains). Der Dehnungskonzentrationstensor wird unabhängig von allen anderen Fasern berechnet. Das heißt, eine Kopplung des Dehnungskonzentrationstensors für jede einzelne Faser an die Situation im umgebenden Verbundwerkstoff wird nicht berücksichtigt. Dadurch geht die Wechselwirkung zwischen Fasern unterschiedlicher Orientierung verloren. In der Full-Mori-Tanaka-Formulierung hingegen wird die Matrix als eine kontinuierliche Phase behandelt. Dies scheint im Hinblick auf den gesunden Menschenverstand näher an der realen Situation im Verbundwerkstoff zu sein.

Rekonstruktion der Orientierungsverteilungsfunktion

Sowohl bei den numerischen als auch bei den analytischen Multiskalen-Modellen ist immer die Kenntnis der lokalen Mikrostruktur im Bauteil erforderlich. Experimentell kann diese z.B. mittels µCT-Messungen ermittelt werden (Bild 5). Dies setzt natürlich schon die Existenz eines Bauteils voraus. Deshalb wird üblicherweise die Faserorientierungsverteilung mittels einer Spritzgießsimulation numerisch ermittelt. Die Spritzgießsimulation liefert die Faserorientierungsverteilung allerdings nur mittelbar über den Orientierungstensor. Aus dem Orientierungstensor muss mittels geeigneter mathematischer Verfahren [2] die räumliche Verteilung der Fasern rekonstruiert werden (Bild 5).

Fazit

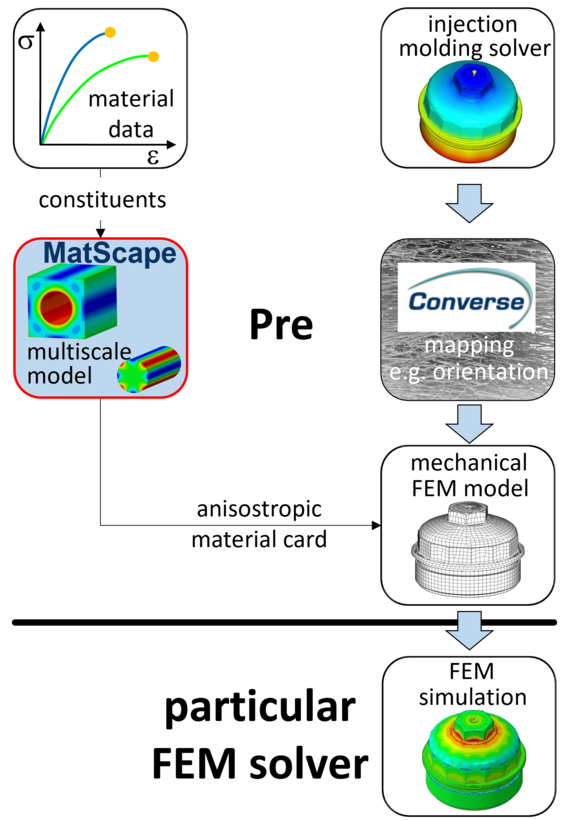
Die 2-Stufen-Homogenisierung auf Basis des Full-Mori-Tanaka-Ansatzes ist in der Multiskalen Software Converse bzw. des Materialmodellierungsmoduls MatScape von PART Engineering für die Bestimmung des linear-elastischen Verhaltens des Verbundwerkstoffs implementiert. Für den linear elastischen Fall ist ein solcher Ansatz rechnerisch sehr effektiv und liefert die elastischen Eigenschaften in guter Übereinstimmung mit Experimenten. Für den plastischen Teil des Materialverhaltens ist jedoch bekannt, dass die Vorhersagefähigkeit der analytischen mikromechanischen Modelle im Allgemeinen schlecht ist. Außerdem impliziert die Berücksichtigung von plastischen Effekten auf der Mikroskala einen inkrementellen numerischen Lösungsansatz des gesamten mikromechanischen Gleichungssatzes, der numerisch sehr aufwändig ist. Daher werden in Converse plastische Effekte durch die Einführung eines orientierungsabhängigen Fließkriteriums berücksichtigt, das bereits für den homogenisierten Verbundwerkstoff definiert ist, was rechnerisch sehr effektiv und im Hinblick auf die Kalibrierung des Modells einfach zu handhaben ist. Es werden so mit Hilfe der in diesem Beitrag vorgestellten analytischen Modellansätze sogenannte pre-homogenized Materialkarten berechnet die dann an den jeweiligen FE-Solver übergeben werden (Bild 6).

Aufgrund der Leistungsfähigkeit des in Converse implementierten hybriden Ansatzes, wurde die Vorgehensweise auch bereits von anderen Autoren in ähnlicher Weise umgesetzt [3]. Dies unterstreicht die Praxistauglichkeit der PART Softwarelösungen.

[1] K. Breuer und M. Stommel, „Prediction of Short Fiber Composite Properties by an Artificial Neural Network Trained on an RVE Database“, Fibers, Bd. 9, Nr. 8, S. 14, 2021, doi: doi.org/10.3390/fib9020008.

[2] K. Breuer, M. Stommel, und W. Korte, „Analysis and Evaluation of Fiber Orientation Reconstruction Methods“, Journal of Composites Science, Bd. 367, Nr. 3, S. 22, 2019, doi: doi:10.3390/jcs3030067.

[3] H. Xu, M. Kuczynska, N. Schafet, F. Welschinger, und J. Hohe, „FE-based damage modeling approach for short fiber reinforced thermoplastics under quasi-static load coupling anisotropic viscoplasticity and matrix degradation“, Journal of COMPOSITE MATERIALS, Bd. 56, Nr. 20, S. 3113–3125, 2022, doi: DOI: 10.1177/00219983221109327.

Autor

Dr. Wolfgang Korte ist Geschäftsführer bei der PART Engineering GmbH, Bergisch Gladbach